Table of Contents

1. 原論文
2. 概要
3. 詳細
   1. 前提知識
   2. Graph Auto-Encoderの定式化
      1. Definitions
      2. Inference model
      3. Generative model
      4. Learning
      5. Non-probabilistic graph auto-encoder (GAE) model
   3. 実験
      1. 比較モデル
      2. 実験手順
      3. 実験結果
   4. 個人的実験

原論文

• タイトル : Variational Graph Auto-Encoders
• 著者 : Thomas N. Kipf and Max Welling
• 論文リンク : https://arxiv.org/abs/1611.07308
• 著者コード : https://github.com/tkipf/gae
• PyTorch geometric(Example) : https://github.com/rusty1s/pytorch_geometric/blob/master/examples/autoencoder.py
• その他 : Bayesian Deep Learning Workshop (NIPS 2016)

概要

• グラフ構造を持つデータに対するAoto Encoderの提案
  • 具体的には「Variational Graph Auto-Encoders」と「Graph Auto-Encoders」の2手法を提案
• 各ノードの分散表現を得る
• Link predictionで従来の手法の精度を超える
• 個人的実験

詳細

前提知識

本節では論文とは独立に、グラフの構造を行列で表現する隣接行列と次数行列について簡単に説明します。 例として下記の図のようにノードが4個、エッジが4本のネットワークを考えます。

このようにノードとエッジで構成される構造をグラフと呼んでいます。またエッジはノード間を繋ぐ線です。友人関係などを想像すると上の構造をイメージできると思います。 ノード1はノード2とノード3とは友人関係にありますが、ノード4とはノード3を介した友達の友達のような関係性です。 次数行列 $D$ は非常に簡単で、それぞれのノードが何本のエッジを有しているかを行列の対角成分に置いた行列のことです。従って今回の例の場合

\begin{align} D = \begin{pmatrix} 2 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 \\ 0 & 0 & 3 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \end{align}

となります。 また、ノード間の繋がりを行列表記したものが隣接行列 $A$ と呼ばれるものです。上のグラフを隣接行列で表現したものが

\begin{align} A = \begin{pmatrix} 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 0 \\ 1 & 1 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{pmatrix} \end{align}

になります。ノード1の友人が誰かを知りたい場合には1行目、または1列目を確認します。ノード2, 3と繋がるエッジとして1がふられており、エッジが構成されていないノード4には0がふられます。このように隣接行列はノードとエッジの関係性を行列で表現したものになります。 上記例では「グラフ構造 -> 隣接行列」の流れで行列を構築しましたが、逆の「隣接行列 -> グラフ構造」を構成することも容易です。

隣接行列は「ノード1はノード4とはノード3を介した友達の友達のような関係性です」も表現することができています。上で紹介した隣接行列は1step先のノードとエッジの関係を表現するものでした。ノード1とノード4は2step先のノードに当たりますが、隣接行列のべき数がstep数と対応します。例えば2step先のノードとの関係性は $A^2$ に対応します。

\begin{align} A^2 &= \begin{pmatrix}0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 0 \\ 1 & 1 & 0 & 1 \\ 0 & 0 & 1 & 0\end{pmatrix} \begin{pmatrix}0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 0 \\ 1 & 1 & 0 & 1 \\ 0 & 0 & 1 & 0\end{pmatrix} \\ &= \begin{pmatrix}2 & 1 & 1 & 1 \\ 1 & 2 & 1 & 1 \\ 1 & 1 & 3 & 0 \\ 1 & 1 & 0 & 1\end{pmatrix} \end{align}

ここで計算した $A^2$ が構成するグラフ構造は

つまり $A^2$ の1行目などは2stepでノード1にたどり着く経路および経路の数を指しています。

ここまでをまとめると

のように対応しており、隣接行列がグラフ構造そのものを定式化したものになっていることがわかると思います。

Graph Auto-Encoderの定式化

論文の本題である Graph Auto-Encoderを論文の記法に従って説明していきます。 モデルの概要としては著者のコードページにある図が非常にわかりやすいです。

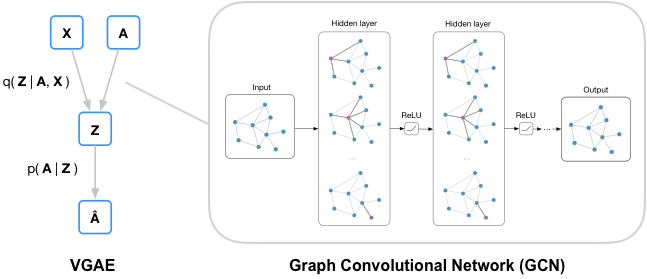
グラフの構造を表現する隣接行列 $A$ とノードの特徴を表現した特徴量行列 $X$ を入力とし、自分自身の隣接行列 $A$ に予測結果の $\hat{A}$ を近づけるAuto-Encoderです。 論文では「Variational Graph Auto-Encoders」と「Graph Auto-Encoders」の2手法を提案しています。

Definitions

グラフを $\mathcal{g} = (\mathcal{V}, \mathcal{E})$ とし $\mathcal{V}$ がノード集合、 $\mathcal{E}$ がエッジ集合を指します。また、ノードは $N(=|\mathcal{V}|)$ 個あります。 また、論文ではここまでに紹介した次数行列・隣接行列の他に特徴量行列 $X$ を導入します。ノードごとの持っている特徴量を並べたテーブルデータになります。例えばノードiの年齢や、ノードiについたラベルデータなどを指します。 ノードごとに特徴量を羅列したものなので $N\times D$ の行列 $X$ になります。

Inference model

Auto-Encoderのモデル全体として隣接行列 $A$ と特徴量行列 $X$ を入力し、潜在変数 $Z$ を推論します。また、Variational Graph Auto-Encoderの文面では $Z$ の事後分布に正規分布を仮定し、KLを最小化します。

\begin{align} q(\mathbf{Z}|\mathbf{X},\mathbf{A}) = \prod_{i=1}^N q(\mathbf{z}_i|\mathbf{X},\mathbf{A}) \quad \text{with} \quad q(\mathbf{z}_i|\mathbf{X},\mathbf{A}) = \mathcal{N}(\mathbf{z}_i| \boldsymbol{\mu}_i, \mathrm{diag}(\boldsymbol{\sigma}_i^2)) \end{align}

ここで $\boldsymbol{\mu} = \mathrm{GCN}_{\boldsymbol \mu} (\mathbf{X}, \mathbf{A})$ 、 $\log\boldsymbol{\sigma} = \mathrm{GCN}_{\boldsymbol{\sigma}}(\mathbf{X}, \mathbf{A})$ で構成されます。ここで登場する $\mathrm{GCN}$ の関数はグラフ畳み込み層を指します。グラフ畳み込み層は下記のような2層のネットワークで構築されます。

\begin{align} \mathrm{GCN}(\mathbf{X}, \mathbf{A}) &= \mathbf{\tilde{A}}\ \mathrm{ReLU}\bigl(\mathbf{\tilde{A}}\mathbf{X}\mathbf{W}_0\bigr)\mathbf{W}_1\\ \mathbf{\tilde{A}} &= \mathbf{D}^{-\frac{1}{2}}\mathbf{A}\mathbf{D}^{-\frac{1}{2}} \end{align}

補足として、次元圧縮する $\mathrm{GCN}(\mathbf{X}, \mathbf{A})$ は $\mathbf{\tilde{A}}$ が $N\times N$ の行列、特徴量行列 $\mathbf{X}$ が $N \times D$ の行列で構成されています。また $\mathbf{W}_i$ は圧縮したい次元に従った大きさになります。ここでは $\mathbf{W}_0$ を $D \times K_0$ 行列、 $\mathbf{W}_1$ を $K_0 \times K$ 行列で構成し、GCN全体として $N \times K$ 行列とします。この一行一行が各ノードの潜在空間でのK次元分散表現とみなすことができます。

Generative model

Auto-Encoderのdecoder側が

\begin{align} p\left(\mathbf{A|\mathbf{Z}}\right) = \prod_{i=1}^N\prod_{j=1}^N p\left(A_{ij}|\mathbf{z}_i,\mathbf{z}_j\right)\quad \text{with} \quad p\left(A_{ij}=1,|,\mathbf{z}_i,\mathbf{z}_j\right) = \sigma(\mathbf{z}_i^\top\mathbf{z}_j) \end{align}

で構成され、 $A_{ij}$ が $\mathbf{A}$ の成分を指し、 $\sigma(\cdot)$ がシグモイド関数を指します。VAEとしてはreconstruction lossに対応します。

Learning

学習では重み行列 $\mathbf{X}$ を更新し、通常のVAE同様KLと再構成誤差の和で変分下界を構成し、最大化します。

\begin{align} \mathcal{L} = \mathbb{E}_{q(\mathbf{Z}|\mathbf{X},\mathbf{A})}\bigl[\log p\left(\mathbf{A}|\mathbf{Z}\right)\bigr] - \mathrm{KL}\bigl[q(\mathbf{Z}|\mathbf{X},\mathbf{A})||p(\mathbf{Z})\bigr] \end{align}

学習自体もVAEと同様に reparametrization trickを使って誤差を伝播させます。

特徴量に当たるデータがない場合には $\mathbf{X}$ に単位行列を置いて同様の操作で学習をします。

Non-probabilistic graph auto-encoder (GAE) model

GVAEは潜在変数の事前分布に確率的な正規分布を仮定して学習をしていきますが、もっと直接的に non-probabilistic な方法で Graph Auto-Encoderをする方法も提案しています。

\begin{align} \mathbf{\hat{A}} = \sigma\bigl(\mathbf{Z} \mathbf{Z}^\top\bigr) \quad \text{with} \quad \mathbf{Z} = \mathrm{GCN}(\mathbf{X}, \mathbf{A}) \end{align}

実験

同様の分散表現を獲得するモデルとLink predictionというタスクを比較し、有用性を確かめています。

比較モデル

• spectral clustering (SC)
• DeepWalk (DW)

SCやDeepWalkの説明は 「グラフの中心でAIを叫んだノード(なおAIは出ない) 〜あるいはnode2vecに至るグラフ理論〜」 で詳しく扱っています。 SCはグラフラプラシアンからノードのグラフフーリエ変換をし、スペクトルを抽出する方法です。DWはノードの繋がりからランダムウォークさせて文章列のようなデータセットをサンプルし、ノードの分散表現を得る方法です。。 それぞれ、今回紹介した隣接行列 $A$ と次数行列 $D$ の情報を利用しているものの、特徴量行列 $X$ の情報をモデルに乗せることはできません。

実験手順

1. グラフ全体から一部のエッジを取り除き、不完全なグラフを構築
2. 1のデータからそれぞれのモデルでノードの分散表現を獲得する
3. 取り除いたデータも含めて2ノード間でエッジが構成されるか学習し予測する。その際の特徴量として分散表現を用いて、(他の論文をみる限り)ロジスティック回帰でテストする

VGAEとGAE

• lr = 0.01
• Adam
• epoch = 200
• dim N -> 32 -> 16 -> N で16次元を分散表現としている

SC

• 原論文の実装
• 128次元

DW

• 原論文の実装
• 128次元
• ノードごとの長さ80
• コンテキストサイズ10のランダムウォークを10回
• 1epoch

実験結果

データセットのCora, Citeseer, Pubmedは論文の引用のネットワークです。特徴量行列には特定の単語の有無を特徴量としています。 document frequencyが10未満の単語の削除にストップワードの削除を行っています。また、stemmingも実行して単語の数を減らしているようです。

個人的実験

弊社社員のストレングスファインダー結果でネットワークを構築し、分散表現を得て、マッチングアルゴリズムを適用しました………が、あまりに個人情報ゆえ内容は非公開で。