大谷選手のホームラン確率を推定
はじめに
本記事では、大谷翔平選手のホームラン確率を、ベイジアンモデリングを用いて推定します。 今回は、大谷選手の打席データを用いて、ホームラン確率を推定する簡易的なモデルを構築し、そのモデルを用いて、様々な打席状況におけるホームラン確率を予測します。 先日、社外の勉強会後の飲み会で「野球は状態が明確に定義された状態でゲームが進むので、ベイズの当てはまりが良い」って入れ知恵をされたので、考えてみました。 全ての内容はGoogle Colabにてまとめました。
精度だけではもしかしたらGBDT系の方が良いかもしれないですが、ざっと思い浮かぶ感じでもベイズをやる意味合いは下記のような観点があると思います。
- データが少ない場合に当てはまりが良い(過去データが少なくても、事前分布が補完する)
- シミュレーションができる(反実仮想としてGBDTだとしてもできる)
- 分布関数として表現できる(工夫しないとGBDTではできない)
- 事前分布となるパラメータに関する事後分布が得られる
- 単純にベイズが使えて満足する
データ
分析には、pybaseball パッケージを用いて、Statcastデータを取得しました。
Statcastデータとは、MLBで導入されているデータ分析システムらしく、投球や打球の軌跡、速度、角度など、様々なデータを取得することができます。
pybaseball では様々な切り口でMLBの選手やチームに関してデータを取得できるのですが、今回は特定の選手の打席のデータを取得します。取得できるカラムはこちらにまとまっています。google翻訳などを使って調べると、なんとなくわかります(自分は野球に詳しいわけじゃないので、よくわからない情報もいくつも。。。)。
流石にcolabでも pybaseball はデフォルトでインストールされていないので、まずはパッケージをインストールします。
!pip3 install --upgrade pybaseball
さらに以降で必要なパッケージをimportします
from pybaseball import statcast_batter
import matplotlib.pyplot as plt
import numpy as np
import polars as pl
import pymc as pm
(colabではnumpy周りのエラーが出ますが、今回の処理で問題はないので、そのまま進んじゃいました)
データの取得
データの取得期間は、2018年3月29日から2024年10月14日(昨日のメッツ戦までの最新のデータ)までです。
# 2018年から現在までの大谷翔平の1球ごとの打席データを取得
data = statcast_batter("2018-03-29", "2024-10-14", player_id=660271)
df = pl.from_pandas(data)
ダウンロードはpandasのデータフレームでreturnされるのですが、なんとなく気分の問題でpolarsに変換しました。 実際に得られるデータは、colabのノートブックにて確認していただければと思います。
簡易分析
大谷選手の2018年からのMLBでの出場試合数は、statcastデータから取得した game_pk カラムの一意な値の数で確認できます。
ホームラン数は、 events カラムが 'home_run' となっているデータの数で確認できます。
# MLBでの出場試合数
print(f"試合数: {len(df['game_pk'].unique())}")
# ホームラン数
print(f"ホームラン数: {len(df.filter(pl.col('events') == 'home_run'))}")
# 試合あたりのホームラン割合
print(f"試合あたりのホームラン割合: {len(df.filter(pl.col('events') == 'home_run')) / len(df['game_pk'].unique())}")
# 打席あたりのホームラン割合
print(f"打席あたりのホームラン割合: {len(df.filter(pl.col('events') == 'home_run')) / len(df)}")
出力
試合数: 916
ホームラン数: 236
試合あたりのホームラン割合: 0.2576419213973799
打席あたりのホームラン割合: 0.016065350578624914
らしいです。4試合に1回はホームランを打っている割合ってすごいですね。 さらに今シーズンはバッターのみに専念しているので、これまでの傾向とそれなりに傾向が変わるだろうと推測しています。ですので、2024年のデータをフィルターしました。
# 今シーズンのみバッターに専念し、特異なデータなはずなので、今年のデータのみでモデリングする
df_2024 = df.filter(pl.col("game_date").str.starts_with("2024-"))
# MLBでの出場試合数
print(f"試合数: {len(df_2024['game_pk'].unique())}")
# ホームラン数
print(f"ホームラン数: {len(df_2024.filter(pl.col('events') == 'home_run'))}")
# 試合あたりのホームラン割合
print(f"試合あたりのホームラン割合: {len(df_2024.filter(pl.col('events') == 'home_run')) / len(df_2024['game_pk'].unique())}")
# 打席あたりのホームラン割合
print(f"打席あたりのホームラン割合: {len(df_2024.filter(pl.col('events') == 'home_run')) / len(df_2024)}")
出力
試合数: 176
ホームラン数: 57
試合あたりのホームラン割合: 0.32386363636363635
打席あたりのホームラン割合: 0.018633540372670808
30%の試合でホームランを打っているようで、さらにすごいですね。 このデータを用いて、以後モデリングを進めていきます。
データの前処理
取得したデータに対して、以下の前処理を行いました。
- ストライクとボールのパターンによって、各パターンをbinaryのデータとしてカラムを作成しました。
- 各ベースに走者がいる場合をbinaryデータとしてカラムに上書きしました。
- ホームランの有無をbinaryデータとして作成しました。
これらの前処理により、モデルへの入力データを作成しました。 データの前処理は下記の通りにまとめています(もっと効率の良いコードはあると思うのですが、、、まぁ。)。
# ストライクとボールのパターンによって「1球見る」的な話聞くし(いつ見るのかとか全然知らない)、全パターンをbinaryのデータとしてカラムを作成
# (もっと頭の良い書き方あるけど、愚直に書いてしまった)
df_2024 = df_2024.with_columns(
(pl.col("strikes").cast(pl.Utf8) + "_" + pl.col("balls").cast(pl.Utf8)).alias("strikes_balls")
).with_columns(
[
pl.when(pl.col("strikes_balls") == "0_0").then(1).otherwise(0).alias("0_0"),
pl.when(pl.col("strikes_balls") == "1_0").then(1).otherwise(0).alias("1_0"),
pl.when(pl.col("strikes_balls") == "2_0").then(1).otherwise(0).alias("2_0"),
pl.when(pl.col("strikes_balls") == "0_1").then(1).otherwise(0).alias("0_1"),
pl.when(pl.col("strikes_balls") == "1_1").then(1).otherwise(0).alias("1_1"),
pl.when(pl.col("strikes_balls") == "2_1").then(1).otherwise(0).alias("2_1"),
pl.when(pl.col("strikes_balls") == "0_2").then(1).otherwise(0).alias("0_2"),
pl.when(pl.col("strikes_balls") == "1_2").then(1).otherwise(0).alias("1_2"),
pl.when(pl.col("strikes_balls") == "2_2").then(1).otherwise(0).alias("2_2"),
pl.when(pl.col("strikes_balls") == "0_3").then(1).otherwise(0).alias("0_3"),
pl.when(pl.col("strikes_balls") == "1_3").then(1).otherwise(0).alias("1_3"),
pl.when(pl.col("strikes_balls") == "2_3").then(1).otherwise(0).alias("2_3"),
# 同様に各ベースに奏者がいる場合をbinaryデータとしてカラムに上書き
# 塁に残っている選手のIDが格納されているので、もし塁に人がいる場合にintにして和をとる
pl.when(pl.col("on_1b").is_null()).then(0).otherwise(1).alias("is_1b"),
pl.when(pl.col("on_2b").is_null()).then(0).otherwise(1).alias("is_2b"),
pl.when(pl.col("on_3b").is_null()).then(0).otherwise(1).alias("is_3b"),
]
)
# 過去のデータ
past_runners_on_base = df_2024.select(
(pl.col("is_1b") + pl.col("is_2b") + pl.col("is_3b")).alias("is_runner")
)["is_runner"].to_numpy()
is_1b = df_2024["is_1b"].to_numpy()
is_2b = df_2024["is_2b"].to_numpy()
is_3b = df_2024["is_3b"].to_numpy()
# 各ストライクとボールのパターンのデータを格納
s_b_0_0 = df_2024["0_0"].to_numpy()
s_b_1_0 = df_2024["1_0"].to_numpy()
s_b_2_0 = df_2024["2_0"].to_numpy()
s_b_0_1 = df_2024["0_1"].to_numpy()
s_b_1_1 = df_2024["1_1"].to_numpy()
s_b_2_1 = df_2024["2_1"].to_numpy()
s_b_0_2 = df_2024["0_2"].to_numpy()
s_b_1_2 = df_2024["1_2"].to_numpy()
s_b_2_2 = df_2024["2_2"].to_numpy()
s_b_0_3 = df_2024["0_3"].to_numpy()
s_b_1_3 = df_2024["1_3"].to_numpy()
s_b_2_3 = df_2024["2_3"].to_numpy()
# アウトカウントを格納
past_outs = df_2024["outs_when_up"].to_numpy()
# ホームランの有無をbinaryデータ作成
past_home_run = df_2024.with_columns(
pl.when(pl.col("events") == "home_run").then(1).otherwise(0).alias("home_run"),
)["home_run"].to_numpy()
モデリング
ベイズの定理
ベイジアンモデリングでは、ベイズの定理に基づいて、データと事前知識を組み合わせて、事後分布を推定します。
$$ p(\theta|{\rm data}) = \frac{p({\rm data}|\theta)p(\theta)}{p({\rm data})} $$- $\theta$ はモデルのパラメータ(ホームラン確率 $p_{\rm season}$ や回帰係数 $\beta_{\rm 1b}$ など)
- $p(\theta∣{\rm data})$ は事後分布で、観測データを考慮した後のパラメータの分布
- $p({\rm data}∣\theta)$ は尤度関数で、観測データがパラメータ $\theta$ の下でどれだけ適合するか
- $p(\theta)$ は事前分布で、観測データを得る前のパラメータに関する知識を表す
事前分布
ホームラン確率 $p_{\rm season}$ は、事前知識に基づいてベータ分布に従うと仮定します。
$$ p_{\rm season} \sim {\rm Beta}(\alpha, \beta),\\ \beta_i \sim {\rm Normal}(\mu=0, \sigma=1) $$ベータ分布の $\alpha$ は過去のホームラン回数、 $\beta$ は過去データの全試行回数を入力します。 正規分布に従う $\beta_i$ は後に導入されるロジスティック回帰の重みの事前分布を指します(ベータ分布の母数 $\beta$ と、重みの $\beta_i$ は変数がかぶってしまっているのですが、全くの別物です。注意してください。)。
打席ごとの状況に基づく確率の計算
打席ごとの状況に応じて、ホームラン確率を調整する。ロジスティック回帰に基づいて推論します。
$$ p = \sigma\Bigl[{\rm logit}(p_{\rm season}) + \beta_0 \\+ \beta_{\rm 1b} \cdot {\rm 1塁の走者の有無}\\ + \beta_{\rm 2b} \cdot {\rm 2塁の走者の有無}\\ +\cdots +\\ \beta_{\rm out} \cdot {\rm アウトカウント}\Bigr] $$ここで $\sigma(x)$ はシグモイド関数。
$$ \sigma(x) = \frac{1}{1 + \exp(-x)} $$さらに ${\rm logit}(x)$ はロジスティック関数。
$$ {\rm logit}(x) = \log\frac{x}{1 - x} $$ロジスティック回帰としては、シーズン全体のホームラン確率(事前確率)を基準に、各打席ごとの特徴量による調整をする形で構成されています。
観測データのモデル化
観測データ $y_i$ (その打席でホームランを打ったかどうか)は、最終的なホームラン確率 $p_{\rm final}$ に従うベルヌーイ分布に従う仮定をします。
$$ y_i \sim {\rm Bernoulli}(p, i) $$これらの設計のもと、MCMCでパラメータをfitします。
# モデルの初期フィット
with pm.Model() as model:
# シーズン全体のホームラン率に基づく事前分布(ベータ分布)
season_rate = pm.Beta("season_rate", alpha=len(df_2024.filter(pl.col('events') == 'home_run')), beta=len(df_2024))
# 回帰係数の事前分布(正規分布)
# 野球のドメイン知識が全然ないので、あまりweightの目安がなく、とりあえず全部一緒
# たぶん今シーズン、全てのシチュエーションが出揃っているわけではない気がするので、事前分布のパラメータが影響してしまうと思う
beta_0 = pm.Normal("beta_0", mu=0, sigma=1)
beta_runners = pm.Normal("beta_runners", mu=0, sigma=1)
beta_1b = pm.Normal("beta_1b", mu=0, sigma=1)
beta_2b = pm.Normal("beta_2b", mu=0, sigma=1)
beta_3b = pm.Normal("beta_3b", mu=0, sigma=1)
beta_0_0 = pm.Normal("beta_0_0", mu=0, sigma=1)
beta_1_0 = pm.Normal("beta_1_0", mu=0, sigma=1)
beta_2_0 = pm.Normal("beta_2_0", mu=0, sigma=1)
beta_0_1 = pm.Normal("beta_0_1", mu=0, sigma=1)
beta_1_1 = pm.Normal("beta_1_1", mu=0, sigma=1)
beta_2_1 = pm.Normal("beta_2_1", mu=0, sigma=1)
beta_0_2 = pm.Normal("beta_0_2", mu=0, sigma=1)
beta_1_2 = pm.Normal("beta_1_2", mu=0, sigma=1)
beta_2_2 = pm.Normal("beta_2_2", mu=0, sigma=1)
beta_0_3 = pm.Normal("beta_0_3", mu=0, sigma=1)
beta_1_3 = pm.Normal("beta_1_3", mu=0, sigma=1)
beta_2_3 = pm.Normal("beta_2_3", mu=0, sigma=1)
beta_out = pm.Normal("beta_out", mu=0, sigma=1)
# ロジスティック回帰の線形和
linear_combination = (
pm.math.logit(season_rate) + # season_rateを線形和に変換してベースラインとして組み込む
beta_0 +
beta_runners * past_runners_on_base +
beta_1b * is_1b +
beta_2b * is_2b +
beta_3b * is_3b +
beta_0_0 * s_b_0_0 +
beta_1_0 * s_b_1_0 +
beta_2_0 * s_b_2_0 +
beta_0_1 * s_b_0_1 +
beta_1_1 * s_b_1_1 +
beta_2_1 * s_b_2_1 +
beta_0_2 * s_b_0_2 +
beta_1_2 * s_b_1_2 +
beta_2_2 * s_b_2_2 +
beta_0_3 * s_b_0_3 +
beta_1_3 * s_b_1_3 +
beta_2_3 * s_b_2_3 +
beta_out * past_outs
)
# シグモイド関数を適用して打席ごとのホームラン確率を計算
# turn at bat = 打席らしい
p_home_run_given_at_bat = pm.math.sigmoid(linear_combination)
# 尤度(観測されたホームランデータに基づくベルヌーイ分布)
likelihood = pm.Bernoulli("likelihood", p=p_home_run_given_at_bat, observed=past_home_run)
# 事後分布のサンプリング
trace = pm.sample(2000, return_inferencedata=True)
pm.plot_trace(trace)
pm.plot_posterior(trace)
plt.show()
上記のコードで下記のMCMCのサンプル結果が可視化ができます。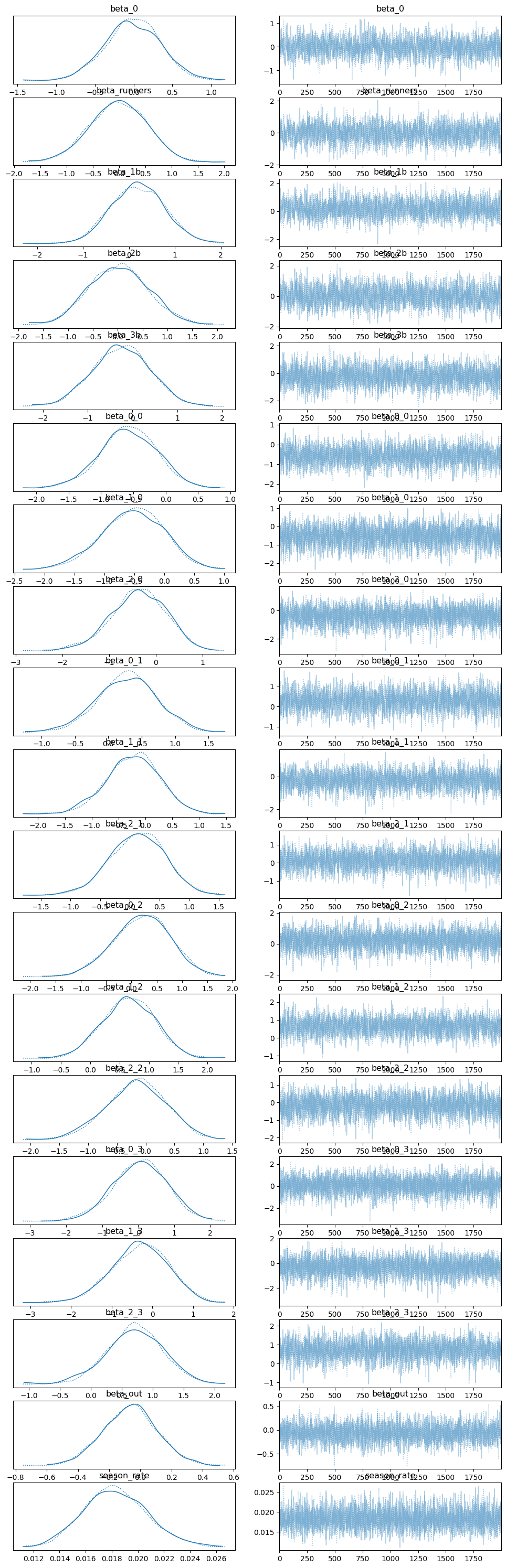
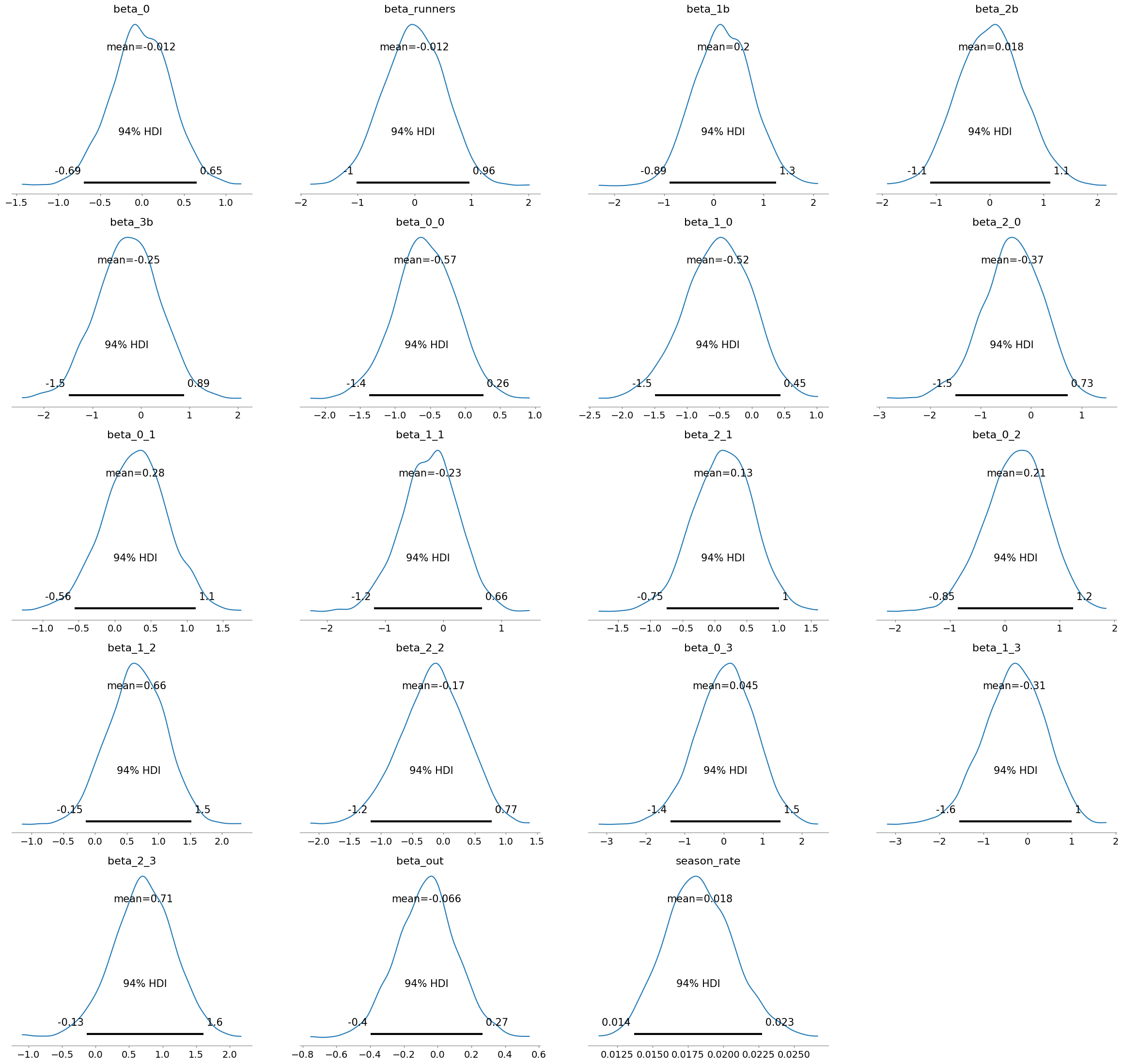
今後のデータに対する推論
ノーアウト走者なしで打席に立ったところな感じで、ホームランの事後確率を推定してみます。
posterior = trace.posterior
# 事後分布からサンプルしたパラメータ
# 例として、traceオブジェクトから事後分布のパラメータを取得
season_rate_samples = posterior["season_rate"].to_numpy().flatten()
beta_0_samples = posterior["beta_0"].to_numpy().flatten()
beta_runners_samples = posterior["beta_runners"].to_numpy().flatten()
beta_1b_samples = posterior["beta_1b"].to_numpy().flatten()
beta_2b_samples = posterior["beta_2b"].to_numpy().flatten()
beta_3b_samples = posterior["beta_3b"].to_numpy().flatten()
beta_0_0_samples = posterior["beta_0_0"].to_numpy().flatten()
beta_1_0_samples = posterior["beta_1_0"].to_numpy().flatten()
beta_2_0_samples = posterior["beta_2_0"].to_numpy().flatten()
beta_0_1_samples = posterior["beta_0_1"].to_numpy().flatten()
beta_1_1_samples = posterior["beta_1_1"].to_numpy().flatten()
beta_2_1_samples = posterior["beta_2_1"].to_numpy().flatten()
beta_0_2_samples = posterior["beta_0_2"].to_numpy().flatten()
beta_1_2_samples = posterior["beta_1_2"].to_numpy().flatten()
beta_2_2_samples = posterior["beta_2_2"].to_numpy().flatten()
beta_0_3_samples = posterior["beta_0_3"].to_numpy().flatten()
beta_1_3_samples = posterior["beta_1_3"].to_numpy().flatten()
beta_2_3_samples = posterior["beta_2_3"].to_numpy().flatten()
beta_out_samples = posterior["beta_out"].to_numpy().flatten()
# 打席の状況を設定(0アウト走者なしで打席に立ったところな感じ)
current_runners_on_base = 0
current_is_1b = 0
current_is_2b = 0
current_is_3b = 0
current_s_b_0_0 = 0
current_s_b_1_0 = 0
current_s_b_2_0 = 0
current_s_b_0_1 = 0
current_s_b_1_1 = 0
current_s_b_2_1 = 0
current_s_b_0_2 = 0
current_s_b_1_2 = 0
current_s_b_2_2 = 0
current_s_b_0_3 = 0
current_s_b_1_3 = 0
current_s_b_2_3 = 0
current_outs = 0
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# 各パラメータに基づくベルヌーイ分布の確率pを計算
# サンプルされたパラメータを使って、新しい打席のホームラン確率を計算
logit_season_rate = np.log(season_rate_samples / (1 - season_rate_samples)) # ロジット変換
p_samples = sigmoid(
logit_season_rate + # season_rate の事後分布
beta_0_samples +
beta_runners_samples * current_runners_on_base +
beta_1b_samples * current_is_1b +
beta_2b_samples * current_is_2b +
beta_3b_samples * current_is_3b +
beta_0_0_samples * current_s_b_0_0 +
beta_1_0_samples * current_s_b_1_0 +
beta_2_0_samples * current_s_b_2_0 +
beta_0_1_samples * current_s_b_0_1 +
beta_1_1_samples * current_s_b_1_1 +
beta_2_1_samples * current_s_b_2_1 +
beta_0_2_samples * current_s_b_0_2 +
beta_1_2_samples * current_s_b_1_2 +
beta_2_2_samples * current_s_b_2_2 +
beta_0_3_samples * current_s_b_0_3 +
beta_1_3_samples * current_s_b_1_3 +
beta_2_3_samples * current_s_b_2_3 +
beta_out_samples * current_outs
)
# pの分布をヒストグラムで可視化
plt.hist(p_samples, bins=50, density=True, alpha=0.75)
plt.title("Posterior Distribution of p (Bernoulli parameter)")
# xは0~0.15までの範囲で表示する
plt.xlim(0, 0.15)
plt.xlabel("p (home run probability)")
plt.ylabel("Frequency")
plt.grid(True)
plt.show()
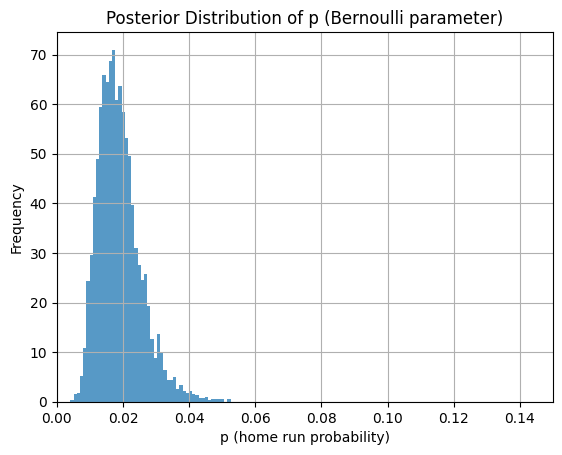
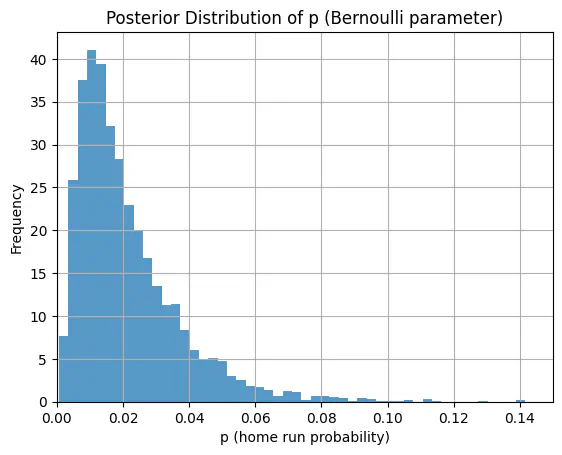
続いて、ノーアウト満塁で打席に立ったところな感じで、ホームランの事後確率を推定してみます。
# 打席の状況を設定(0アウト満塁で打席に立ったところな感じ)
current_runners_on_base = 3
current_is_1b = 1
current_is_2b = 1
current_is_3b = 1
current_s_b_0_0 = 0
current_s_b_1_0 = 0
current_s_b_2_0 = 0
current_s_b_0_1 = 0
current_s_b_1_1 = 0
current_s_b_2_1 = 0
current_s_b_0_2 = 0
current_s_b_1_2 = 0
current_s_b_2_2 = 0
current_s_b_0_3 = 0
current_s_b_1_3 = 0
current_s_b_2_3 = 0
current_outs = 0
# 各パラメータに基づくベルヌーイ分布の確率pを計算
p_samples = sigmoid(
logit_season_rate + # season_rate の事後分布
beta_0_samples +
beta_runners_samples * current_runners_on_base +
beta_1b_samples * current_is_1b +
beta_2b_samples * current_is_2b +
beta_3b_samples * current_is_3b +
beta_0_0_samples * current_s_b_0_0 +
beta_1_0_samples * current_s_b_1_0 +
beta_2_0_samples * current_s_b_2_0 +
beta_0_1_samples * current_s_b_0_1 +
beta_1_1_samples * current_s_b_1_1 +
beta_2_1_samples * current_s_b_2_1 +
beta_0_2_samples * current_s_b_0_2 +
beta_1_2_samples * current_s_b_1_2 +
beta_2_2_samples * current_s_b_2_2 +
beta_0_3_samples * current_s_b_0_3 +
beta_1_3_samples * current_s_b_1_3 +
beta_2_3_samples * current_s_b_2_3 +
beta_out_samples * current_outs
)
# pの分布をヒストグラムで可視化
plt.hist(p_samples, bins=50, density=True, alpha=0.75)
plt.title("Posterior Distribution of p (Bernoulli parameter)")
# xは0~0.15までの範囲で表示する
plt.xlim(0, 0.15)
plt.xlabel("p (home run probability)")
plt.ylabel("Frequency")
plt.grid(True)
plt.show()
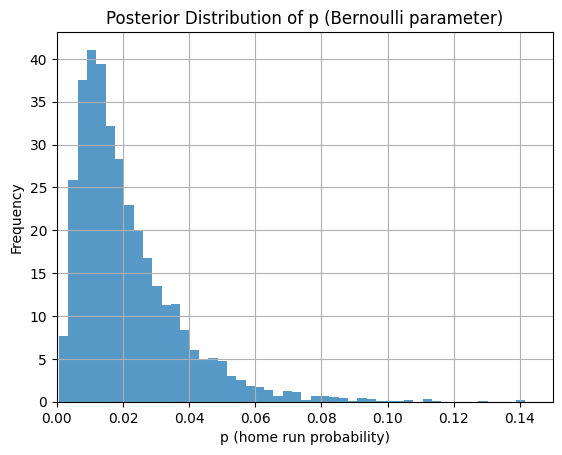
間違えていなければ「ノーアウト走者なし」と「ノーアウト満塁」だと満塁の方が事後確率のテイルが広いっぽいです(確率が大きくなり得る)。
1日程度で組んだコードなので、どこかにミスがあるかもです。見つけた際には教えていただけると幸いです。
後に調べて知りましたが、上記のpymcのコードは色々改善の余地がありそうです。。。 https://zenn.dev/yoshida0312/articles/bbd246d3da42b3
お疲れ様でした。